Cover Letter:
|
Baker’s Choice provides open-ended questions that allow for complex thinking and most importantly, the application of already understood mathematical concepts. The depth of understanding was reached through collaboration and strategically placed guided questions. Students found reasoning in meaningful ways to make sense of the bigger picture. Baker’s Choice is an Interactive Mathematics Program (IMP) unit for replacing about three weeks of student practice with graphs and equations in a traditional algebra, advanced algebra, or even geometry or pre-calculus class. The problems within the book make you think hard and it helps with learning about real-world problems, inequalities, problem solving skills, strategies, and more.
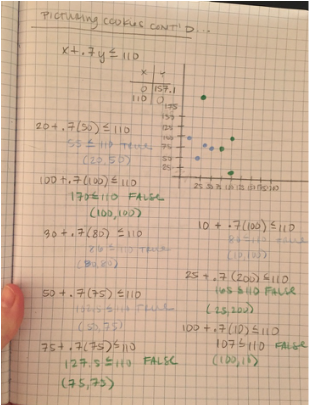
The Bakers Choice unit covers problems that allow students to see the effects and implications of linear equations and linear inequalities and how they can be applied to linear programming. I believe the central problem of the unit was Picturing Cookies. In Picturing Cookies, students become familiar with what graphing inequalities actually means by plotting points that satisfy a given constraint in one color and don't satisfy the constraint in another. Picturing Cookies was the first problem for students to tackle regarding linear programming. The problem required students to investigate how many combinations of plain and iced cookies can be created with given constraints. Plain and iced cookies are being sold with certain limitations. The limitations (constraints) are as follows: Total amount of cookie dough: 110 lbs • 1 dozen plain cookies: 1 lb • 1 dozen iced cookies: 0.7 lbs Total amount of icing: 32 lbs • 1 dozen iced cookies: 0.4 lbs Total amount of oven space: • 140 dozen cookies maximum Total amount of time they have to make cookies: 15 hours • 1 dozen plain cookies: 0.1 hours • 1 dozen iced cookies: 0.15 hours Profit: • 1 dozen plain cookies: $1.50/dozen • 1 dozen iced cookies: $2.00/dozen Using these inequalities, x represents the amount of plain cookies while y represents the amount of iced cookies. We can represent these constraints as follows: Cookie Dough: x + 0.7y is less than or equal to 110 Icing: 0.4y is less than or equal to 32 Oven Space: x + y is less than or equal to 140 Time: 0.1x + 0.15y is less than or equal to 15 From here, we graphed our constraints. From our graph we were able to determine all possible combinations of plain and iced cookies and construct a feasible region, which meets all the constraints. Using this information we saw how to find the maximum profit with the equation P= $1.50x + $2.00y. As we saw in this unit the maximum profit will occur at one vertex of the shaded region or one entire side of the figure. This is because of the slope of the profit line. After connecting that the maximum profit is at a vertex (or along the constraint line), students can use the profit equation to figure out where the profit is maximized. They know the information to plug in by looking at the feasible region and the vertices. The Baker's Choice unit is great for students because it focuses on critical thinking and students communicating that thinking in order for them to develop a deeper level of understanding. Though this unit is focused on linear programming, teaching this type of learning process to students can help them in all their future math courses. |
Selected Papers:
My portfolio contains the selected papers of:
- Homework 15: Beginning Portfolio Selection
- POW: Kick It!
- Picturing Pictures
- POW: A Marching Strip
- Baker’s Choice Revisited
Homework 15:
|
Steps to solve a linear programming problem:
In tackling linear programming problems, I first read through the problem a few times and highlight, underline and circle any information I believe to be important. From there, I begin to identify what my constraints are and represent them symbolically. After I identified the variables and written the constraint inequalities, I graph the constraints using different colors for each constraint. At the end of graphing, I shade the area that makes the inequality true. I develop the profit equation based off the information provided and plug in the points of the vertices of the feasible region. When I plug these in, I can find the maximum profit. 3 Activities:
POW: Kick It!Problem: In Kick It!, students are to figure out what the highest impossible score is for the Free Thinkers Football League when each field goal counts for 5 points and each touchdown counts for 3 points. The football league can score with a combination of a field goal and a touchdown, or just one kind of score.
Process: I created a table and started listing numbers. I started at 1 and ended at 30. Right away I knew that 1 and 2 were impossible scores as the smallest amount of points possible is 3. I also knew that 4 was impossible because 3(2) or 3+3 would never get you to 4 and the other point possible started at 5 points. I was able to get to every number through 30 except for 1, 2, 4 and 7. Solution: 7 is the highest impossible number. I know this because I went all the way up through 30 and once you get to 30, you know you can add 10 to every number after 30 and still get a number that works. I know this because 5(2)=10. 7 is the highest impossible score because after 7, all numbers can be subtracted by 5 or 3 to evenly equal 0. |
Picturing Pictures:
|
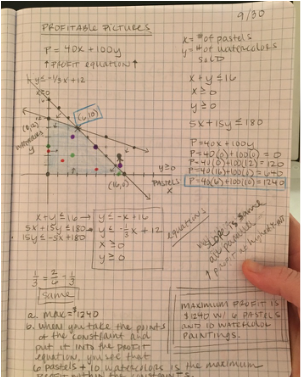
Problem: In Picturing Pictures, an artist, Hassan, is preparing for a street fair where he will sell his paintings. Hassan creates watercolor and pastel paintings. Though each type of painting takes about the same amount of time, the resources and costs differ. Hassan can make, at most, 16 paintings. His pastel paints cost $5 each and his watercolor paintings cost him $15 in materials and he has $180 to spend on materials. Hassan makes a profit of $40 on each pastel painting and $100 for each watercolor painting. Students are to use symbols to represent Hassan's constraints, make a graph and graph at least 5 points representing the profit Hassan could make on his paintings.
Process: I started off by representing Hassan's constraints with symbols. I used "x" to represent the number of pastels and "y" to represent the number of watercolors. Number of pictures Hassan can make: x + y is less than or equal to 16 Number of pastels: x is greater than or equal to 0 Number of watercolors: y is greater than or equal to 0 Cost of materials: 5x + 15y is less than or equal to 180 Profit = 40x + 100y From here, I graphed several points and showed Hassan's feasible region and then analyzed the combination of watercolors and pastels that satisfy Hassan's constraints. Solution: The maximum profit for Hassan is $1240 with 6 pastel paintings and 10 watercolor paintings. |
POW: A Marching Strip
|
Problem: A king wants a new rectangular courtyard that will be laid out with tiles, all in the shape of squares. He chose tiles that look good and are reasonably priced. The problem
is that visiting dignitaries only walk at a diagonal that goes from one corner
of the courtyard to the opposite corner. Because of this, the tiles along the
diagonal will get much more use than the other tiles and would need to be replaced
because they are cheaper tiles. The solution would be to purchase and put more
expensive and heavy-duty tiles along the diagonal. Every tile that contains a
segment of the diagonal must be the more durable, expensive tile. If a tile is
touching the diagonal at a corner, it can be the less expensive tile.The king wants a 63x90 courtyard and wants to know how many expensive tiles he will need to cover the diagonal path of his courtyard. The king also wants to know if he were to change his mind on the size of his courtyard, is there a general formula he could apply to figure out how many expensive tiles he would need.
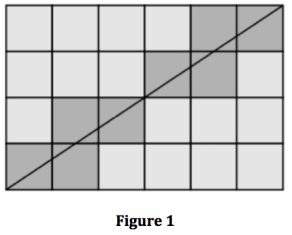
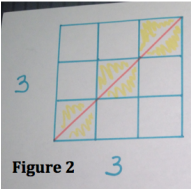
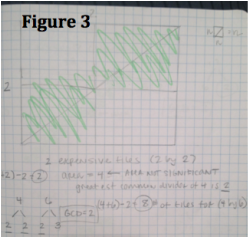
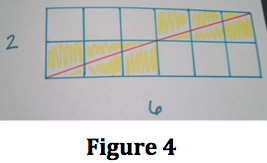
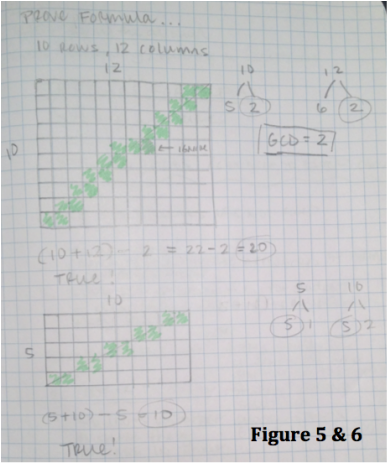
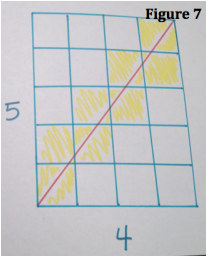
Process: Right off the bat, I started working off of the figure the problem provided me with (Figure 1, a 4x6 courtyard). My first instinct was to work with the area of the courtyard, which was 24. This courtyard needs 8 expensive tiles and I know that 8 goes into 24 evenly 3 times. But what does 3 have to do with the number or rows and columns? Not anything that I could see. The row and column’s greatest common factor is 2, but how does that relate to 8? It goes into 8 four times and 2x4=8. Does that work? I put the idea of working with area off to the side to try another approach. I then looked at the rows and columns to see if they had anything in common. 4 and 6 are both divisible by 2, which is also their greatest common factor. Is there a way we can arrive at the number of tiles using the greatest common factor of the rows and columns? I assumed there had to be some significance to knowing the number of columns and rows. I knew that the number of expensive tiles needed was 8, so how do I get to 8 using the number of rows and columns and GCF? Then I added 4 and 6 and arrived at 10. 10-8=2 and 2 is the GCF. I think I might have found a pattern! I decided to try my idea on a different courtyard layout. I started with 3x3. 3 is the greatest common factor of 3 and that 3+3=6-3=3. When I drew the courtyard (with an accurate scale), I saw that we needed 3 expensive tiles and that worked! So two of my courtyards worked with my conjecture to do with adding rows and columns and subtracting their GCD. I continued and drew out three more courtyards with varying dimensions and came to find that my conjecture worked for all three. Now that was all with even number. What if I had an even amount of columns and odd amount of columns? It still works, even when the GCD is 1. I then went back to the main question: how many expensive tiles will the king need for a 63x90 courtyard? Solution: I came up with the formula: (R + C) – GCD = number of expensive tiles needed. That is, I add the number of rows and columns together and then subtract their GCD, in order to determine how many expensive tiles would be needed. Figure 1: 4x6 à (4 + 6) – 2 = 8 expensive tiles needed. Figure 2: 3x3 à (3 + 3) – 3 = 3 expensive tiles needed. Figure 3: 2x2 à (2 + 2) – 2 = 2 expensive tiles needed. Figure 4: 2x6 à (2 + 6) – 2 = 6 expensive tiles needed. Figure 5: 10x12 à (10 + 12) – 2 = 20 expensive tiles needed. Figure 6: 5x10 à (5 + 10) – 5 = 10 expensive tiles needed. Figure 7: 5x4 à (5 + 4) – 1=8 expensive tiles needed. Then I applied the formula to the initial question. If the king designed a 63x90 courtyard, he would need 144 expensive tiles. I arrived at this answer because (63 + 90) – 9 = 14 |
Baker's Choice Revisited:
Plain and iced cookies are being sold with certain limitations. The constraints are as follows:
Total amount of cookie dough: 110 lbs
• 1 dozen plain cookies: 1 lb
• 1 dozen iced cookies: 0.7 lbs
Total amount of icing: 32 lbs
• 1 dozen iced cookies: 0.4 lbs
Total amount of oven space:
• 140 dozen cookies maximum
Total amount of time they have to make cookies: 15 hours
• 1 dozen plain cookies: 0.1 hours
• 1 dozen iced cookies: 0.15 hours
Profit:
• 1 dozen plain cookies: $1.50/dozen
• 1 dozen iced cookies: $2.00/dozen
Using these inequalities, x represents the amount of plain cookies while y represents the amount of iced cookies.
We can represent these constraints as follows:
Cookie Dough: x + 0.7y is less than or equal to 110
Icing: 0.4y is less than or equal to 32
Oven Space: x + y is less than or equal to 140
Time: 0.1x + 0.15y is less than or equal to 15
After graphing the constraints, we can see the feasible region that consists of the vertices at the points (30, 80) and (75,50), (0,80), and (110,0). Now that we know the vertices, we use our profit equation of P= $1.50x + $2.00y, which we also graph.
After putting in each coordinate, we discover that the maximum profit is at (75,50) and will make the Woos $212.50.
75 dozen plain cookies and 50 dozen iced cookies gives a maximum profit of $212.50.
Total amount of cookie dough: 110 lbs
• 1 dozen plain cookies: 1 lb
• 1 dozen iced cookies: 0.7 lbs
Total amount of icing: 32 lbs
• 1 dozen iced cookies: 0.4 lbs
Total amount of oven space:
• 140 dozen cookies maximum
Total amount of time they have to make cookies: 15 hours
• 1 dozen plain cookies: 0.1 hours
• 1 dozen iced cookies: 0.15 hours
Profit:
• 1 dozen plain cookies: $1.50/dozen
• 1 dozen iced cookies: $2.00/dozen
Using these inequalities, x represents the amount of plain cookies while y represents the amount of iced cookies.
We can represent these constraints as follows:
Cookie Dough: x + 0.7y is less than or equal to 110
Icing: 0.4y is less than or equal to 32
Oven Space: x + y is less than or equal to 140
Time: 0.1x + 0.15y is less than or equal to 15
After graphing the constraints, we can see the feasible region that consists of the vertices at the points (30, 80) and (75,50), (0,80), and (110,0). Now that we know the vertices, we use our profit equation of P= $1.50x + $2.00y, which we also graph.
After putting in each coordinate, we discover that the maximum profit is at (75,50) and will make the Woos $212.50.
75 dozen plain cookies and 50 dozen iced cookies gives a maximum profit of $212.50.
Statement of Personal Growth:
I have to say, the first day of Math Methods was a bit overwhelming. Majority of my peers are of the mathematician type (math majors) while I am this architecture major that is good at math, but I approach problems in a much more simple manner in comparison to my peers. At the beginning of the semester I thought this was a major disadvantage but at this point in time, I see it as an advantage. I am teaching kids, not math majors. The ability to break down a complex problem and describe it in a simple and understandable language is of great asset as a math teacher and to those children that have a very difficult time understanding math and are often frustrated.
Baker’s Choice is not something I had heard of before but I think it’s an excellent book and strategy to incorporate in my future classroom. From Driscoll’s book, that we also read this semester, I started thinking about how students think. As a teacher, we need to reflect on how they think and then analyze how that thinking guides our teaching. When tackling activities in Baker’s Choice, I know how I would solve it but with Driscoll's examples of students' work, I can visualize how students might see a problem. I would definitely use Baker’s Choice in my classroom. Being able to fully explain and reason my thinking, organization, process, and answer, I have a better understanding of mathematics than those who can get the answer but have difficulty explaining what everything means and justify their process and solution. I’ve come to realize in my classes as well as the classes I’ve observed, that students have a hard time explaining their process and their thinking.
Baker’s Choice and this course got me to a level of conceptual understanding that I would not have been able to reach alone. I was asked to think in a way that we want our students to think and it was a great eye-opening experience to just how frustrating these tasks can be. The most challenging day was when you asked us to solve a problem only knowing a few mathematically concepts (mirrored exactly what my kids actually know) and to solve a linear programming problem. It was extremely difficult for me to tackle a problem with limited knowledge but it was the best way for me to understand where my students’ minds are. We cannot forget that we are teaching children and we cannot assume that they just know certain things or have a number sense synonymous to our own.
This course has helped me develop much better listening skills. Another difficult activity that we did was when we were asked to just listen to our partner. I have never been asked to do that and it was exceptionally hard not to make a comment here or there. But it was the best way to understand the mathematical thinking of my partner without trying to influence her with my thinking or ideas.
Reflecting back on my progress as a student and future teacher, I gained a lot of insight on teaching and students. I feel I am in a much better position and I am much more confident in my ability to teach children.
Baker’s Choice is not something I had heard of before but I think it’s an excellent book and strategy to incorporate in my future classroom. From Driscoll’s book, that we also read this semester, I started thinking about how students think. As a teacher, we need to reflect on how they think and then analyze how that thinking guides our teaching. When tackling activities in Baker’s Choice, I know how I would solve it but with Driscoll's examples of students' work, I can visualize how students might see a problem. I would definitely use Baker’s Choice in my classroom. Being able to fully explain and reason my thinking, organization, process, and answer, I have a better understanding of mathematics than those who can get the answer but have difficulty explaining what everything means and justify their process and solution. I’ve come to realize in my classes as well as the classes I’ve observed, that students have a hard time explaining their process and their thinking.
Baker’s Choice and this course got me to a level of conceptual understanding that I would not have been able to reach alone. I was asked to think in a way that we want our students to think and it was a great eye-opening experience to just how frustrating these tasks can be. The most challenging day was when you asked us to solve a problem only knowing a few mathematically concepts (mirrored exactly what my kids actually know) and to solve a linear programming problem. It was extremely difficult for me to tackle a problem with limited knowledge but it was the best way for me to understand where my students’ minds are. We cannot forget that we are teaching children and we cannot assume that they just know certain things or have a number sense synonymous to our own.
This course has helped me develop much better listening skills. Another difficult activity that we did was when we were asked to just listen to our partner. I have never been asked to do that and it was exceptionally hard not to make a comment here or there. But it was the best way to understand the mathematical thinking of my partner without trying to influence her with my thinking or ideas.
Reflecting back on my progress as a student and future teacher, I gained a lot of insight on teaching and students. I feel I am in a much better position and I am much more confident in my ability to teach children.